Functoriality and Naturality

Functoriality

Functor

A (covariant) functor between categories and is a mapping of objects to objects and morphisms to morphisms such that for all -objects and :

A contravariant functor is a similar mapping , but reverses the direction of morphisms:

• ,
• ,
• .

Equivalently, a contravariant functor is a (covariant) functor from the opposite category to .

e.g.

• Every category has an identity functor .
• The mapping sends any vector space to its dual space , and any linear map to its dual map (i.e. the pullback) is a contravariant functor from the category of vector spaces to itself.
• Let be the category of finite sets, and be the category of commutative The functor that sends each finite set to its power set and each function to the corresponding function on the power sets is a contravariant functor.

The Category of Small Categories

We have another example of a category, namely , the category of all small categories and corresponding functors.

Injective and Surjective Functor

A functor is said to be injective on objects if the object part is injective, it is surjective on objects if is surjective. Similarly, is injective or surjective on morphisms if the morphism part is injective or surjective.

Faithful Functor

Functor is faithful if for all , the map is injective.

Full Functor

Functor is full if for all , the map is surjective.

Embedding

A functor is called an embedding if it is full, faithful, and injective on objects.

Definition

Def Full Subcategory A full subcategory consists of some objects of and all of the morphisms between them.

Representable Structure

Representable Functor

Let be a locally small category, we have the representable functors: for all objects .

Definition

Def Generator A generator for category is an object has the property that for any objects and and morphisms f, if then there is an arrow such that . That is, the arrows in the category are distinguished by their effect on generalized elements based at .

Definition

Def Contravariant Representable Functors Let be a locally small category, we have the contravariant representable functors: taking to by for .

Naturality

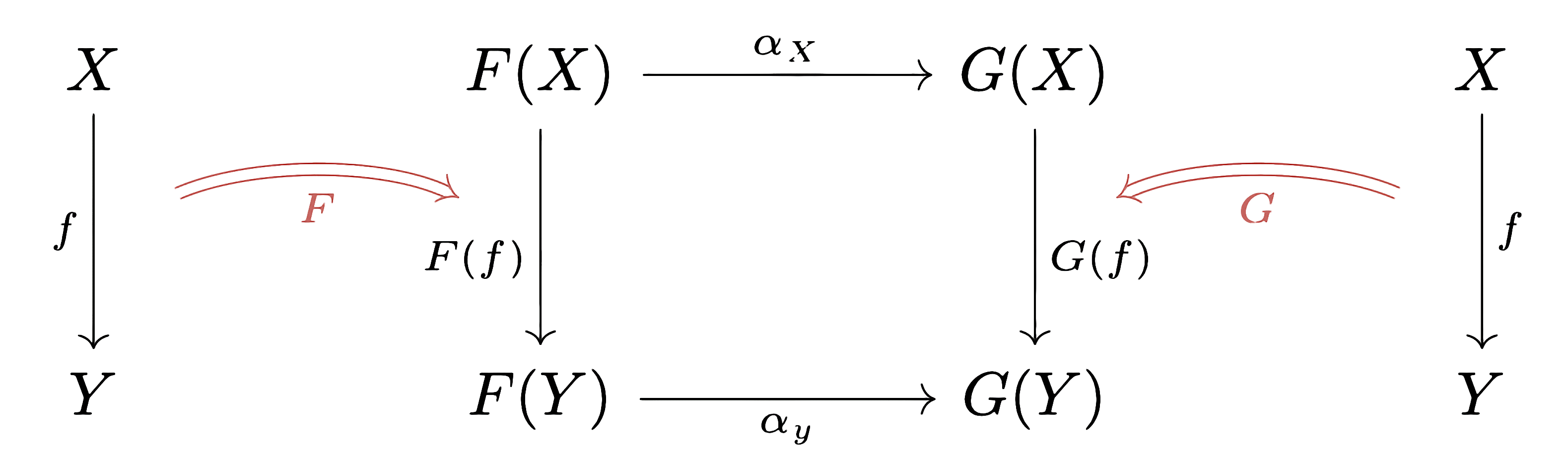
Natural Transformation

Given categories and and covariant functors , a natural transformation consists of:

• morphisms , is called the component of at .
• and components must be such that for every morphism  in  we have:

Vertical Composition

Suppose and are natural transformations between parallel functors . Then there is a natural transformation whose components which is defined to be the vertical composition of the components of and .

Proof Naturality of and implies that for any in the domain category, each square, and thus also the composite rectangle, commutes:

Functor Category

Define the category of functors having functors as objects and natural transformations as arrows. And for each functor object , the natural transformation has components And the composite natural transformation of and is the vertical composition.

Proposition

If categories and are small, then is again a small category, but if and are locally small, then need not be. This is only guaranteed if is locally small and is small.

Natural Isomorphism

A natural isomorphism is a natural transformation in which every component is an isomorphism. In this case, the natural isomorphism may be depicted as

Lemma

A natural transformation is a natural isomorphism if and only if it forms an isomorphism in the functor category.

Lemma

Lemma Given locally small categories , , and , a map of arrows and objects, forms a functor iff

• is functorial in each argument: and are functors for all and .
• satisfies the following interchange law. Given and , .

Proposition

Prop is cartesian closed, with the exponentials . Proof

Equivalence of Categories

Definition

Def Equivalent Categories An equivalence of categories consists of a pair of functors and and a pair of natural isomorphisms In this situation, the functor is called a pseudo-inverse of . The categories and are then said to be equivalent, written .

Proposition

Prop The following conditions on a functor are equivalent:

• is part of an equivalence of categories.
• is full and faithful and “essentially surjective” on objects: for every there is some such that .