Convex Functions

Convex Functions

Def Convex Function A function is convex if is a convex set and for all

Def Strictly Convex A function is strictly convex if is a convex set and for all

Def Strongly Convex A convex function is strongly convex if it has minimum positive curvature everywhere. That is is strongly convex on if there exists an such that

Def Concave Function A function is concave if is convex.

Prop Affine functions are convex and concave; All norms are convex.

Thrm A function is convex if and only if the function that is convex for any

Def Extended-Value Extension The extended-value extension of is

Convex Conditions

Thrm is differentiable if is open and the gradient exists at each .

Thrm First-Order Condition A differentiable with convex domain is convex iff:

Thrm is twice differentiable if is open and the Hessian exists at each

Thrm Second-Order Condition For twice differentiable with convex domain, is convex if and only if for all .

Operations that Preserve Convexity

Comment

Practical methods for establishing convexity of a function

1. Verify definition (often simplified by restricting to a line).
2. For twice differentiable functions, show .
3. Show that is obtained from simple convex functions by operations that preserve convexity.

Def Perspective The perspective of a function is the function such that

Legendre Transformation

The conjugate or Legendre transformation of a convex function is

Proposition

The Legendre transformation is involutive: for convex .

Proof

Young's Inequality

Suppose is convex, then

Lemma

The values of a quadratic form and of its Legendre transformation coincide at corresponding points:

Proof

Prop Operations that Preserve Convexity

• Nonnegative Multiple: is convex if is convex and
• Sum: is convex if convex (extends to infinite sums, integrals)
• Composition with Affine Function: is convex if is convex.
• Pointwise Maximum: if are convex, then is convex.
• Pointwise Supremum: if is convex in for each , then is convex.
• Composition with Scalar Map: Suppose and and , then is convex if either
  • convex, convex, nondecreasing
  • concave, convex, nonincreasing
• Composition with Vector Map: Suppose and and , then is convex if either
  • convex, convex, nondecreasing
  • concave, convex, nonincreasing
• Perspective Transformation: The perspective of is convex if is convex.
• Conjugate: The conjugate of a function is always convex.

Epigraph and Sublevel Set

Def Sublevel Set The -sublevel set of is

Prop Sublevel sets of convex functions are convex.

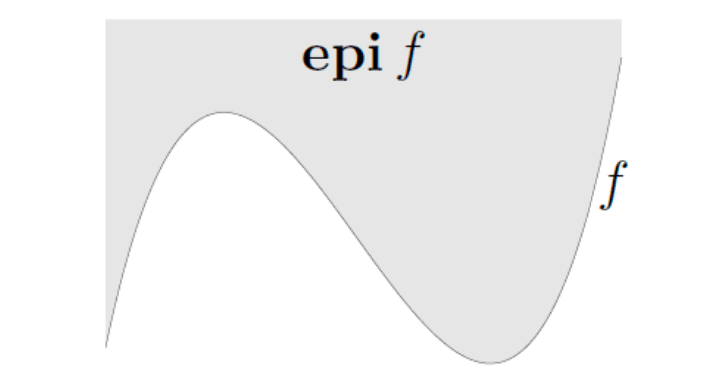
Epigraph

The epigraph of is

Prop is convex if and only if is a convex set

Quasiconvex

Quasiconvex

is quasiconvex if is convex and the sublevel sets are convex for all . Equivalently, is quasiconvex if for all and we have We say is strictly quasiconvex if

Def Quasiconcave is quasiconcave if is quasiconvex.

Prop All convex functions are quasiconvex.

Def Quasilinear is quasilinear if it is quasiconvex and quasiconcave.

Thrm Modified Jensen Inequality Function is quasiconvex if and only if:

Thrm First-order Condition Differentiable with convex domain is quasiconvex if and only if:

Prop Sums of quasiconvex functions are not necessarily quasiconvex

Generalized Convexity

Def is -convex if is convex and for all . e.g. , is -convex.