Holonomic Constraints
Holonomic Constraint
A holonomic constraint of an
particle system is a constraint equation of the form: And so can be written as an equation between coordinates.
Remark
The cool thing about holonomic constraints is that they reduce the degrees of freedom of the system.
e.g.
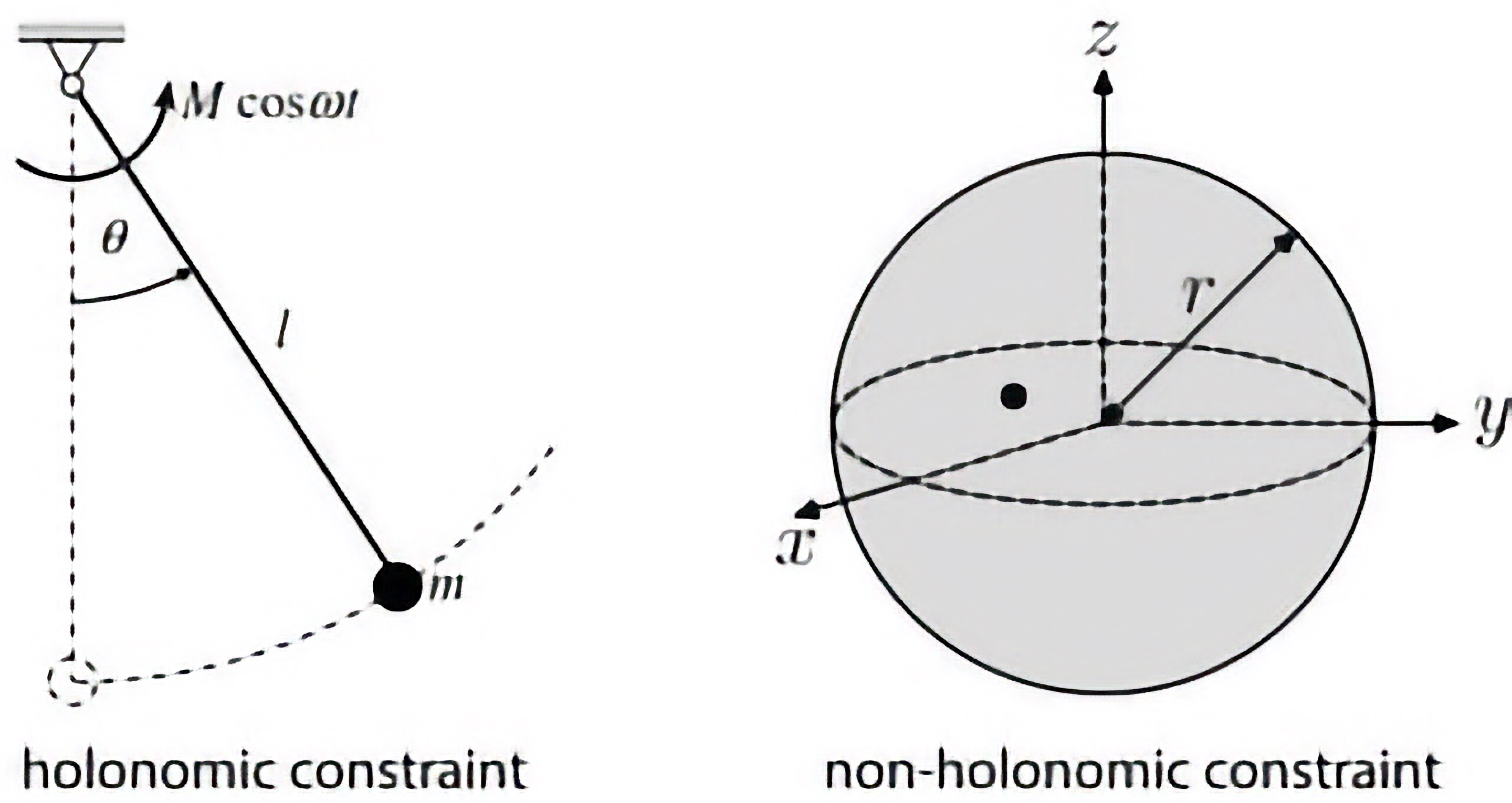
System with Holonomic Constraints
Let
be an -dimensional surface in the -dimensional configuration space of the points with masses . Let be some generalized coordinates, the system described by is called a system of points with ideal holonomic constraints. Or explicitly, using the Lagrange multipliers and the original generalized coordinate and holonomic constraints , the equations of motion are:
Remark
The meaning of these constraints in mechanics lies in the experimentally determined fact that many mechanical systems belong to this class more or less exactly.
Degrees of Freedom
The dimension of the configuration space is called the number of degrees of freedom.
Lagrangian Dynamical System
Lagrangian Dynamical System
A Lagrangian dynamical system is a pair
, where is a smooth manifold, is a smooth function on its tangent bundle. A curve is called a motion in the Lagrangian dynamical system if is an extremal of the functional
e.g. The configuration space of a planar double pendulum is the 2-torus
Natural Lagrangian System
A Lagrangian dynamical system
is called natural if is a Riemannian manifold with metric , and is the difference between the kinetic energy and the potential energy: where is smooth.