Convex Sets

Convex and Affine Set

Line in Euclidean Space

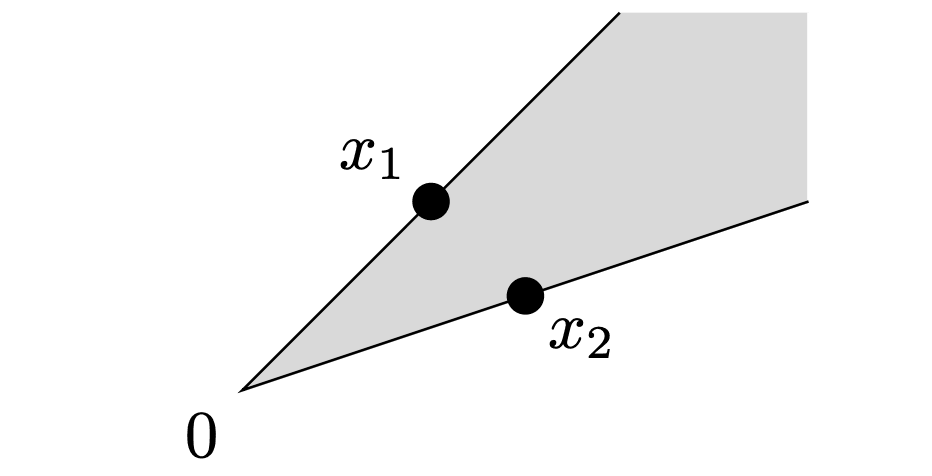
A line through two points is defined as A line segment between two points is defined as

Affine Set

An affine set contains the line through any two distinct points in the set:

e.g. An entire 2D plane.

Theorem

Every affine set can be expressed as the solution set of a system of linear equations.

Convex Set

Let be a vector space. A subset of is convex if whenever and , we have �. That is it contains the line segment between any two distinct points in the set:

e.g.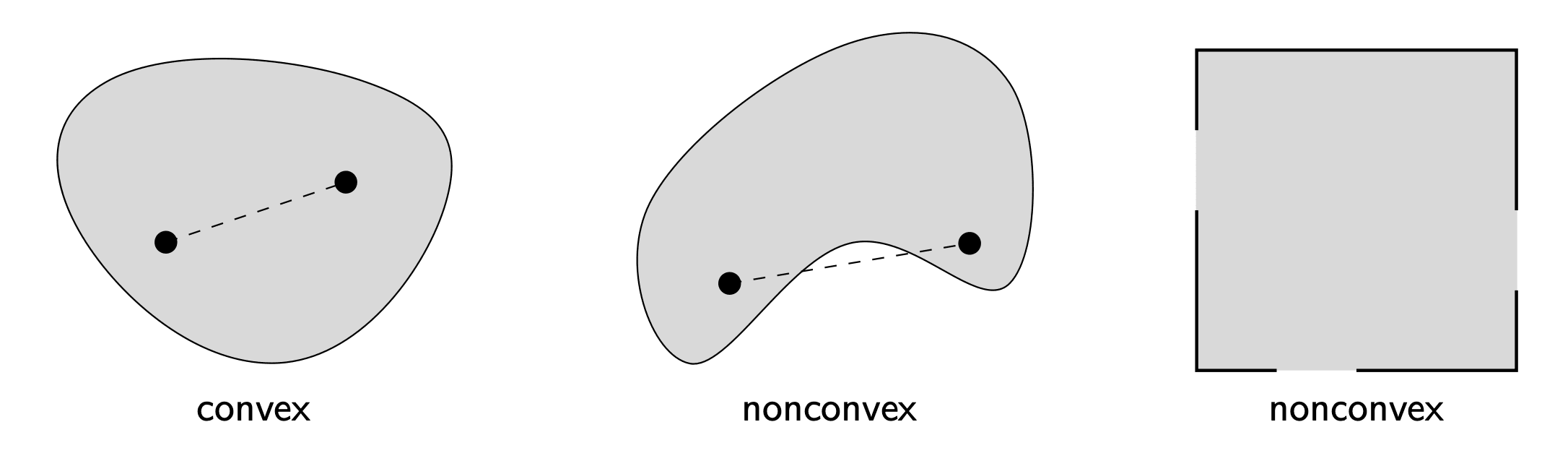

Convex Combination

A convex combination of is any point of the form:with and .

Convex Hull

The convex hull of a set of points , denoted , is the set of all convex combinations of the points in .

Proposition

The convex hull is the smallest convex set to contain all the points in the set .

Cones

Convex Cone

Conic Combination

A conic combination of points and is any point of the form: with and .

Cone

A cone is a set containing all non-negative multiples of its points:

Convex Cone

A convex cone is a set containing all conic combinations of its points.

Proper Cone

A convex cone is a proper cone if

• is closed (contains its boundary)
• is solid (has nonempty interior)
• is pointed (contains no line i.e. )

e.g.

• Nonnegative orthant is a proper cone.
• Positive semidefinite matrices is a proper cone.
• Second-order cone is proper.

Dual Cone

The dual cone of a cone is

Positive Semidefinite Cone

Real Symmetric Matrices

We have the following notation for real symmetric matrices:

• is the set of symmetric matrices
• : positive semidefinite matrices:
• : positive definite matrices

Proposition

Prop iff all eigenvalues are real and nonnegative.

Proposition

Prop is a convex cone.

Hyperplanes, Halfspaces and Polyhedron

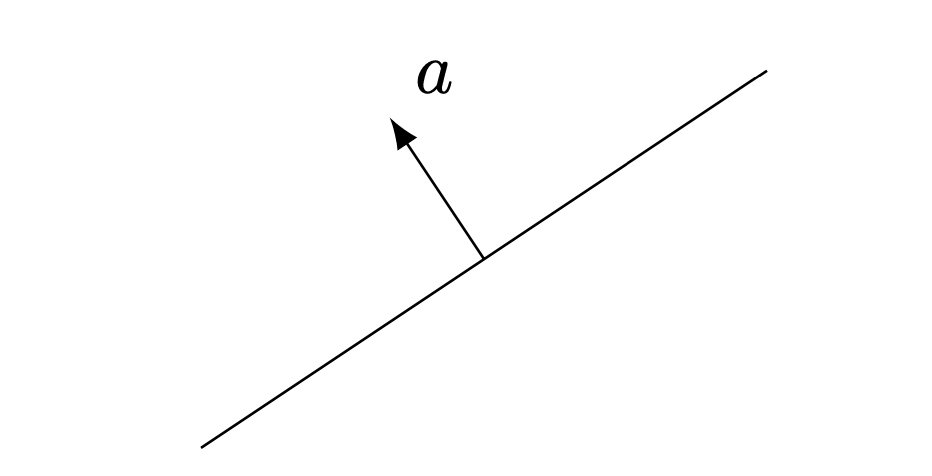
Hyperplane

A hyperplane is a set of the form with . And we call the normal vector.

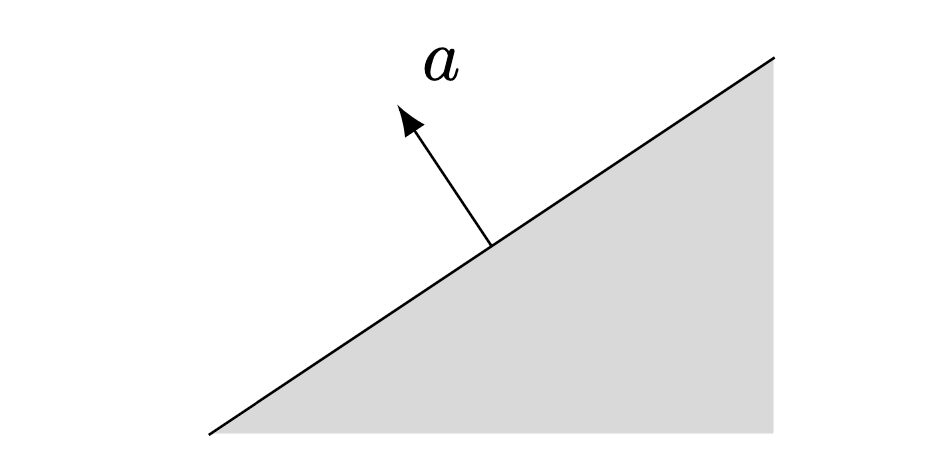
Halfspace

Halfspace is a set of the form with .

Prop Convexity of Hyperplane and Halfspace Hyperplanes are affine and convex, while halfspaces are convex.

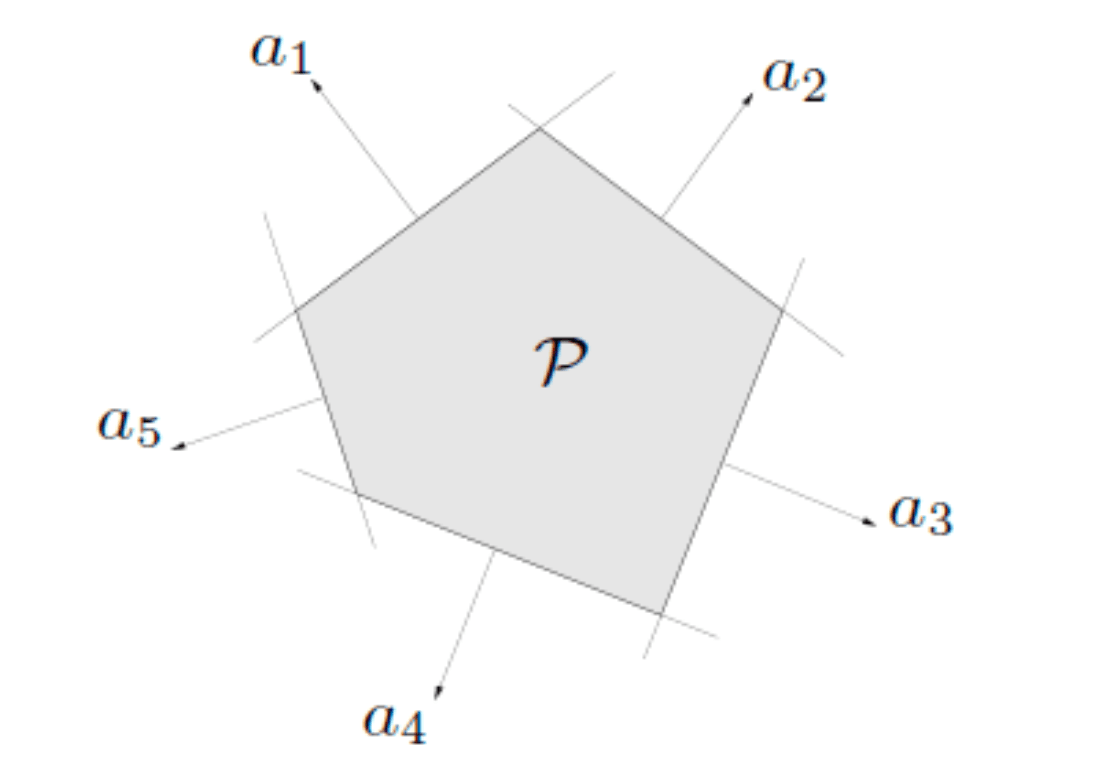
Polyhedron

A polyhedron is the intersection of a finite number of halfspaces and hyperplanes.

Proposition

A polyhedron is the solution set of finitely many linear inequalities and equalities: where , , is component-wise inequality.

Polytope

A polytope is a bounded polyhedron, i.e. a polyhedron with a finite number of extreme points. Equivalently, it is the convex hull of a finite number of points.

Balls and Norm

Euclidean Balls and Ellipsoids

Def Euclidean Ball A (Euclidean) ball with centre and radius is a set of the form:

Def Ellipsoid An ellipsoid is a set of the form:

where (i.e. is symmetric positive definite) Alternatively, we can represent an ellipsoid as with A square and nonsingular.

Norm Balls and Norm Cones

Def Norm Cone A norm ball with centre and radius is the set . A norm cone is the set . The Euclidean norm cone is also called the second-order cone.

Prop Norm balls and norm cones are convex.

Summary of Common Convex Sets

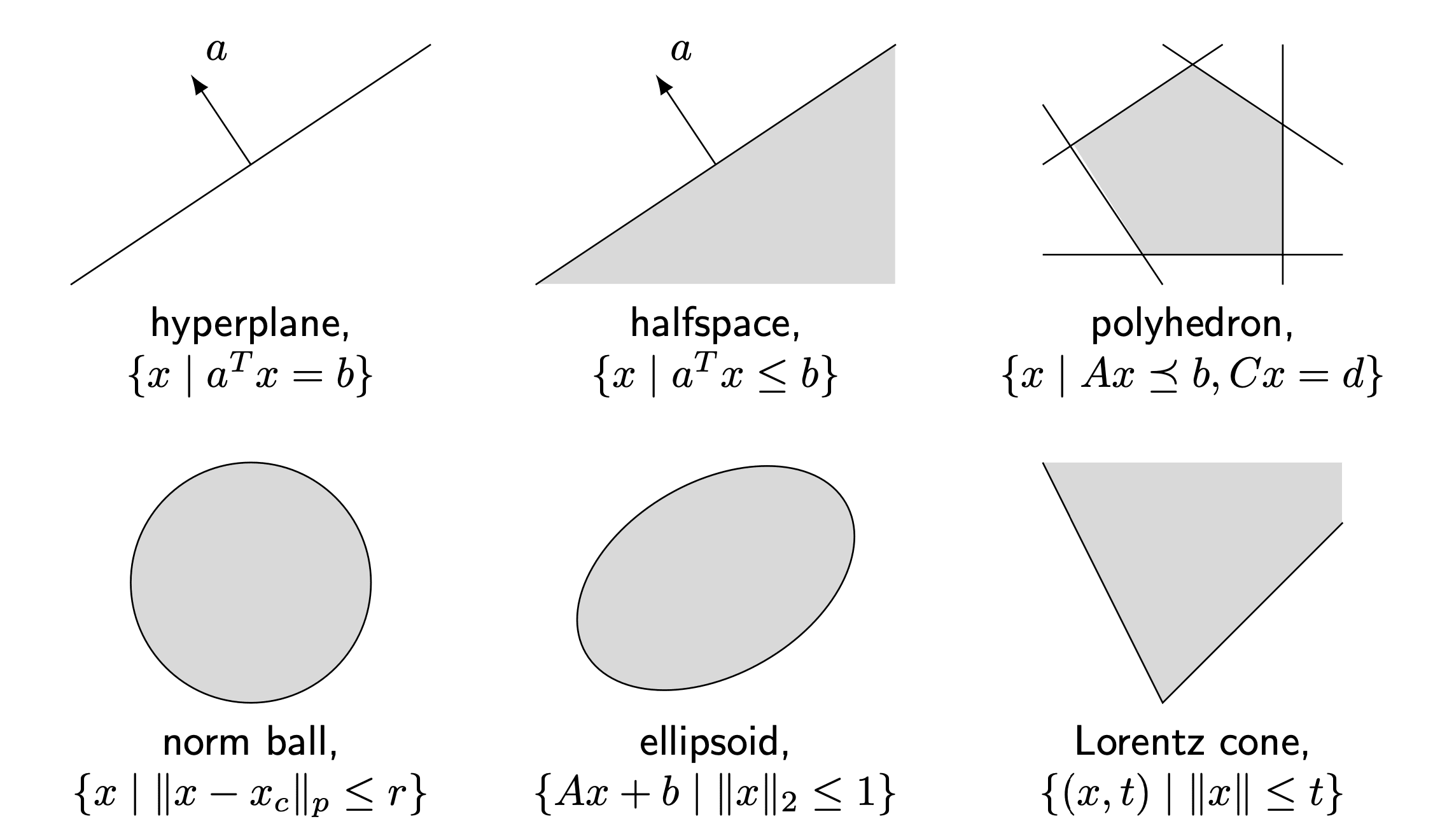
Operations that Preserve Convexity

Proposition

The intersection of arbitrarily many convex sets is convex.

Def Affine Function A function is affine if with , .

Prop The image of a convex set under affine function is convex:

Proposition

The inverse image of a convex set under affine function is convex:

Perspective Function

A perspective function is defined as:

Prop Images and inverse images of convex sets under perspective are convex.

Def Linear-Fractional Function A linear-fractional function is defined as:

Prop Images and inverse images of convex sets under linear-fractional functions are convex.

Generalized Inequalities

Generalized Inequality

A generalized inequality relation defined by a proper cone satisfies where denotes the interior of .

Prop is a partial order, but not in general a linear order.

Prop .

Minimum

is the minimum element of with respect to if

Minimal

is a minimal element of with respect to if (for any)

e.g. Here . is the minimum element of ; is a minimal element of

Proposition

Minimum if exists, must be unique; however, several minimals may be found for  given an generalized inequality  induced by a proper cone .

Separating Hyperplane Theorem

If and are nonempty disjoint convex sets, there exists and such thatThat is the hyperplane separates and .

Supporting Hyperplane Theorem

A supporting hyperplane to set at boundary point iswhere and for all . And if is convex, then there exists a supporting hyperplane at every boundary point of .