The Riemann Sphere

In fact there exists a biholomorphic map between the unit disk and the upper half plane . To see why this should be the case, we will turn to a new perspective on the complex plane.

Riemann Sphere and Stereographic Projection

The Riemann sphere is the complex plane with an additional point added, satisfying We define the stereographic projection as the map by and its inverse as

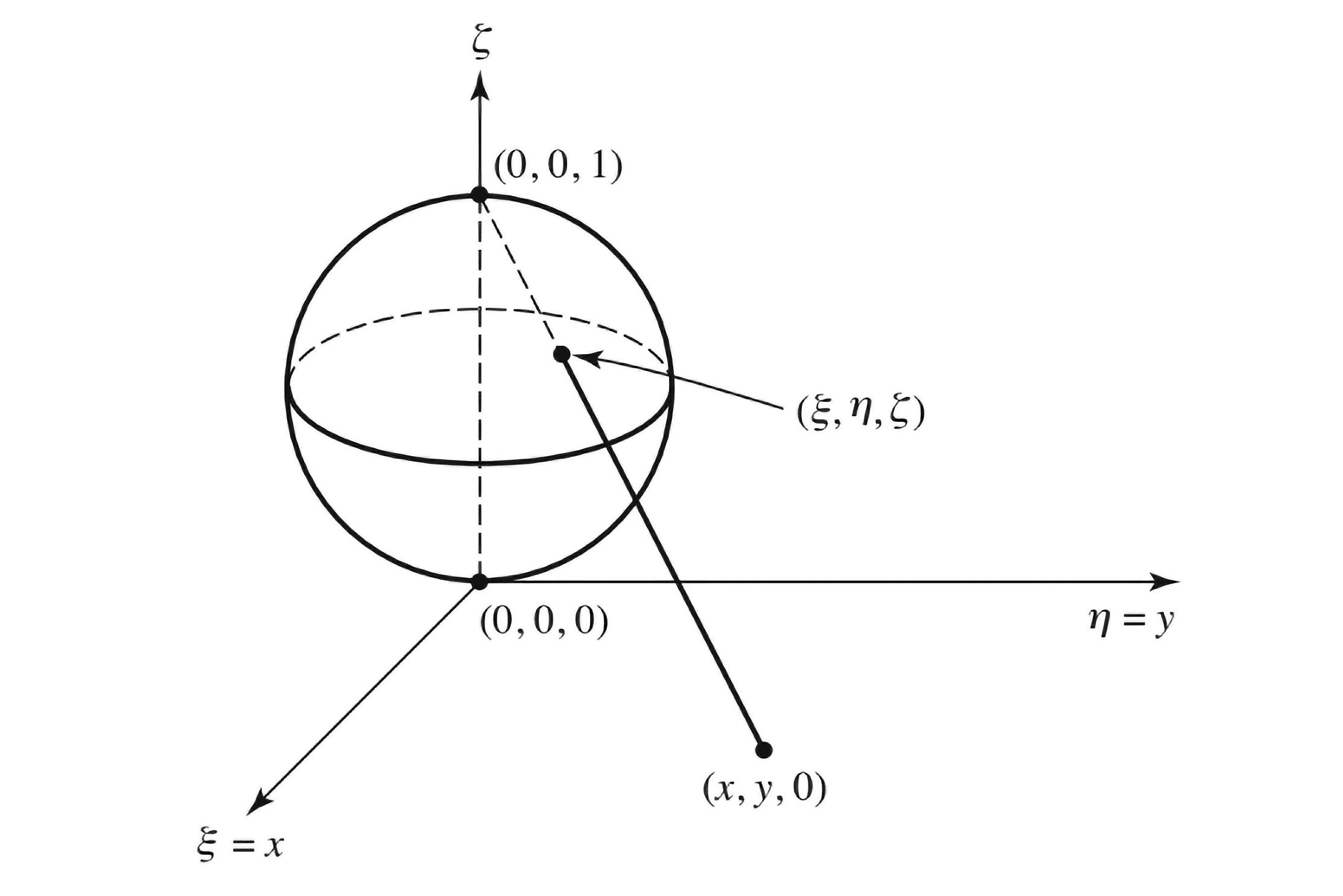
We will not discuss rigorously about the sphere , but you can have an idea of what angle between curves on its surface is. A key feature of stereographic projection is:

Proposition

The stereographic projection is conformal.

So if we have a conformal map , then is a conformal map . An obvious map to think about is the map , which is a degree rotation of the sphere, exchanging and .

Continuous, Differentiable and Conformal on

If is a domain, and , , we say that is continuous/-differentiable/conformal at if one of the following holds:

• and , and is continuous/-differentiable/conformal at in the usual sense.
• but , and is continuous/-differentiable/conformal at .
• but , and is continuous/-differentiable/conformal at .
• and , and is continuous/-differentiable/conformal at .

e.g. Consider . Case , , so it is -differentiable at all points in , in addition, the derivative is non-zero everywhere except at , hence it is conformal on . Case , , so we consider which maps to , and is -differentiable at with derivative , hence it is -differentiable at but not conformal.